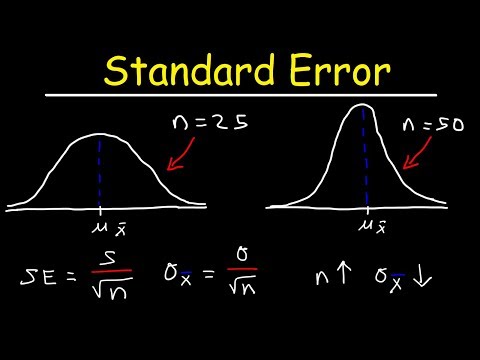
De standaardfout geeft aan hoe verspreid de metingen binnen een gegevensmonster zijn. Het is de standaarddeviatie gedeeld door de vierkantswortel van de steekproefgrootte. De steekproef kan gegevens van wetenschappelijke metingen, testscores, temperaturen of een reeks willekeurige getallen bevatten. De standaardafwijking geeft de afwijking aan van de steekproefwaarden van het steekproefgemiddelde. De standaardfout is omgekeerd evenredig met de steekproefgrootte: hoe groter de steekproef, hoe kleiner de standaardfout.
Bereken het gemiddelde van uw gegevensmonster. Het gemiddelde is het gemiddelde van de steekproefwaarden. Als bijvoorbeeld weerswaarnemingen in een periode van vier dagen gedurende het jaar 52, 60, 55 en 65 graden Fahrenheit zijn, dan is het gemiddelde 58 graden Fahrenheit: (52 + 60 + 55 + 65) / 4.
Bereken de som van de gekwadrateerde afwijkingen (of verschillen) van elke steekproefwaarde van het gemiddelde. Merk op dat het vermenigvuldigen van negatieve getallen zelf (of het kwadrateren van de getallen) positieve getallen oplevert. In het voorbeeld zijn de gekwadrateerde afwijkingen (58 - 52) ^ 2, (58 - 60) ^ 2, (58 - 55) ^ 2 en (58 - 65) ^ 2, respectievelijk 36, 4, 9 en 49 . Daarom is de som van de gekwadrateerde afwijkingen 98 (36 + 4 + 9 + 49).
Zoek de standaarddeviatie. Deel de som van de gekwadrateerde afwijkingen door de steekproefgrootte min één; neem dan de vierkantswortel van het resultaat. In het voorbeeld is de steekproefgrootte vier. Daarom is de standaarddeviatie de vierkantswortel van, die ongeveer 5,72 is.
Bereken de standaardfout, de standaardafwijking gedeeld door de vierkantswortel van de steekproefgrootte. Om het voorbeeld af te sluiten, is de standaardfout 5,72 gedeeld door de vierkantswortel van 4, of 5,72 gedeeld door 2 of 2,86.