Wetten van slingerbeweging

Inhoud

• TL; DR (te lang; niet gelezen)
• Simpele harmonische beweging
• Wetten van een eenvoudige slinger
• Eenvoudige slingerafleiding
• Factoren die de slingerbeweging beïnvloeden
• Lengte van het slingervoorbeeld
• Eenvoudige slingerdefinitie
• Newton Wetten in Pendels

Slingers hebben interessante eigenschappen die natuurkundigen gebruiken om andere objecten te beschrijven. De planetaire baan volgt bijvoorbeeld een vergelijkbaar patroon en slingeren op een schommel kan het gevoel hebben dat je op een slinger zit. Deze eigenschappen komen uit een reeks wetten die de beweging van de slinger regelen. Door deze wetten te leren, kun je beginnen met het begrijpen van enkele basisprincipes van fysica en van beweging in het algemeen.

TL; DR (te lang; niet gelezen)

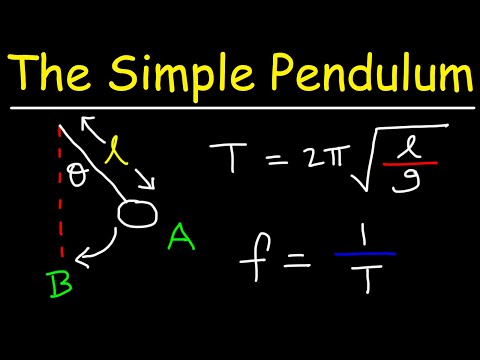
De beweging van een slinger kan worden beschreven met behulp van θ (t) = θ_maxcos (2πt / T) waarin θ vertegenwoordigt de hoek tussen de string en de verticale lijn in het midden, t staat voor tijd, en T is de periode, de tijd die nodig is om een ​​volledige cyclus van de beweging van de pendels te laten plaatsvinden (gemeten door 1 / f), van de motie voor een slinger.

Simpele harmonische beweging

Simpele harmonische beweging, of beweging die beschrijft hoe een objectensnelheid evenredig oscilleert met de hoeveelheid verplaatsing vanuit evenwicht, kan worden gebruikt om de vergelijking van een slinger te beschrijven. Een slinger met een slinger wordt in beweging gehouden door deze kracht die erop inwerkt terwijl deze heen en weer beweegt.

••• Syed Hussain Ather

De wetten die de slingerbeweging regelen, hebben geleid tot de ontdekking van een belangrijke eigenschap. Natuurkundigen verdelen krachten in een verticale en een horizontale component. In slingerbeweging, drie krachten werken direct op de slinger: de massa van de bob, zwaartekracht en de spanning in de snaar. Massa en zwaartekracht werken beide verticaal naar beneden. Omdat de slinger niet omhoog of omlaag beweegt, annuleert de verticale component van de snaarspanning de massa en zwaartekracht.

Dit laat zien dat de massa van een slinger niet relevant is voor zijn beweging, maar de horizontale snaarspanning wel. Eenvoudige harmonische beweging is vergelijkbaar met cirkelvormige beweging. U kunt een object beschrijven dat in een cirkelvormig pad beweegt, zoals weergegeven in de bovenstaande afbeelding door de hoek en straal te bepalen die het in het bijbehorende cirkelvormige pad neemt. Vervolgens kun je met behulp van de trigonometrie van de juiste driehoek tussen het middelpunt van de cirkels, de positie van de objecten en de verplaatsing in beide richtingen x en y, vergelijkingen vinden x = rsin (θ) en y = rcos (θ).

De eendimensionale vergelijking van een object in eenvoudige harmonische beweging wordt gegeven door x = r cos (ωt). U kunt verder vervangen EEN voor r waarin EEN is de amplitude, de maximale verplaatsing van de beginpositie van de objecten.

De hoeksnelheid ω met betrekking tot tijd t voor deze hoeken θ is gegeven door θ = ωt. Als u de vergelijking vervangt die hoeksnelheid en frequentie relateert f, ω = 2πf_, je kunt je deze cirkelvormige beweging voorstellen, dan, als onderdeel van een slinger die heen en weer slingert, dan is de resulterende eenvoudige harmonische bewegingsvergelijking _x = A cos (2πft).

Wetten van een eenvoudige slinger

••• Syed Hussain Ather

Pendels, zoals massa's op een veer, zijn voorbeelden van eenvoudige harmonische oscillatoren: Er is een herstellende kracht die toeneemt afhankelijk van hoe verplaatst de slinger is, en hun beweging kan worden beschreven met behulp van de eenvoudige harmonische oscillatorvergelijking θ (t) = θ_maxcos (2πt / T) waarin θ vertegenwoordigt de hoek tussen de string en de verticale lijn in het midden, t staat voor tijd en T is de periode, de tijd die nodig is om een ​​volledige cyclus van de beweging van de pendels te laten plaatsvinden (gemeten door 1 / f), van de motie voor een slinger.

θ_max is een andere manier om het maximum te definiëren dat de hoek oscilleert tijdens de beweging van de pendels en is een andere manier om de amplitude van de pendels te definiëren. Deze stap wordt hieronder uitgelegd onder de sectie "Eenvoudige pendulumdefinitie."

Een andere implicatie van de wetten van een eenvoudige slinger is dat de oscillatieperiode met constante lengte onafhankelijk is van grootte, vorm, massa en materiaal van het object aan het einde van de snaar. Dit wordt duidelijk aangetoond door de eenvoudige slingerafleiding en de vergelijkingen die het gevolg zijn.

Eenvoudige slingerafleiding

U kunt de vergelijking voor a bepalen eenvoudige slinger, de definitie die afhangt van een eenvoudige harmonische oscillator, uit een reeks stappen die beginnen met de bewegingsvergelijking voor een slinger. Omdat de zwaartekracht van een slinger gelijk is aan de kracht van de slingerbeweging, kunt u ze gelijk aan elkaar instellen met behulp van de tweede wet van Newton met een slingermassa M, draadlengte L, hoek θ, zwaartekrachtversnelling g en tijdsinterval t.

••• Syed Hussain Ather

U stelt de tweede wet van Newton gelijk aan het traagheidsmoment I = mr²_ voor wat massa _m en straal van de cirkelvormige beweging (lengte van de string in dit geval) r maal de hoekversnelling α.

Er zijn andere manieren om een ​​eenvoudige slingerafleiding te maken. Begrijp de betekenis achter elke stap om te zien hoe ze gerelateerd zijn. Je kunt een eenvoudige slingerbeweging beschrijven met behulp van deze theorieën, maar je moet ook rekening houden met andere factoren die de eenvoudige slingertheorie kunnen beïnvloeden.

Factoren die de slingerbeweging beïnvloeden

Als u het resultaat van deze afleiding vergelijkt θ (t) = θ_maxcos (t (L / g)²) naar de vergelijking van een eenvoudige harmonische oscillator (_θ (t) = θ_maxcos (2πt / T)) b_y door ze gelijk aan elkaar te stellen, kun je een vergelijking afleiden voor de periode T.

Merk op dat deze vergelijking T = 2π (L / g)^-1/2 hangt niet van de massa af M van de slinger, de amplitude θ_max, noch op de tijd t. Dat betekent dat de periode onafhankelijk is van massa, amplitude en tijd, maar in plaats daarvan afhankelijk is van de lengte van de string. Het geeft je een beknopte manier om slingerbewegingen uit te drukken.

Lengte van het slingervoorbeeld

Met de vergelijking voor een periode T = 2π (L / g) __^-1/2, kunt u de vergelijking herschikken om L = (T / 2_π) te verkrijgen² / g_ en vervang 1 sec voor T en 9,8 m / s² voor g verkrijgen L = 0,0025 m. Onthoud dat deze vergelijkingen van de eenvoudige slingertheorie aannemen dat de lengte van de snaar wrijvingsloos en massaloos is. Om met die factoren rekening te houden, zouden ingewikkelder vergelijkingen nodig zijn.

Eenvoudige slingerdefinitie

U kunt de slinger naar achteren trekken θ om het heen en weer te laten slingeren om het te zien oscilleren, net als een veer. Voor een eenvoudige slinger kun je het beschrijven met behulp van bewegingsvergelijkingen van een eenvoudige harmonische oscillator. De bewegingsvergelijking werkt goed voor kleinere hoekwaarden en amplitude, de maximale hoek, omdat het eenvoudige pendelmodel afhankelijk is van de benadering die sin (θ) ≈ θ voor wat slingerhoek θ. Aangezien de waarden hoeken en amplitudes groter worden dan ongeveer 20 graden, werkt deze benadering ook niet.

Probeer het zelf maar eens. Een slinger die slingert met een grote beginhoek θ zal niet zo regelmatig oscilleren zodat u een eenvoudige harmonische oscillator kunt gebruiken om het te beschrijven. Bij een kleinere beginhoek θ, de slinger nadert veel gemakkelijker een regelmatige, oscillerende beweging. Omdat de massa van een slinger geen invloed heeft op zijn beweging, hebben natuurkundigen bewezen dat alle slingers dezelfde periode hebben voor oscillatiehoeken - de hoek tussen het middelpunt van de slinger op het hoogste punt en het middelpunt van de slinger op de stoppositie - minder dan 20 graden.

Voor alle praktische doeleinden van een slinger in beweging, zal de slinger uiteindelijk vertragen en tot stilstand komen vanwege de wrijving tussen de snaar en het bevestigde punt erboven, evenals vanwege de luchtweerstand tussen de slinger en de lucht eromheen.

Voor praktische voorbeelden van slingerbeweging zouden de periode en snelheid afhangen van het gebruikte type materiaal dat deze voorbeelden van wrijving en luchtweerstand zou veroorzaken. Als u berekeningen uitvoert op het theoretische oscillerende slingergedrag zonder rekening te houden met deze krachten, dan zal dit een slinger verklaren die oneindig oscilleert.

Newton Wetten in Pendels

De eerste wet van Newton bepaalt de snelheid van objecten in reactie op krachten. De wet stelt dat als een object met een specifieke snelheid en in een rechte lijn beweegt, het oneindig lang met die snelheid en in een rechte lijn zal blijven bewegen, zolang er geen andere kracht op werkt. Stel je voor dat je een bal recht vooruit gooit - de bal zou keer op keer over de aarde gaan als luchtweerstand en zwaartekracht er niet op inwerken. Deze wet laat zien dat, aangezien een slinger heen en weer beweegt en niet op en neer, er geen op en neer krachten op werken.

De tweede wet van Newton wordt gebruikt bij het bepalen van de netto kracht op de slinger door de zwaartekracht gelijk te stellen aan de kracht van de snaar die terug op de slinger trekt. Als u deze vergelijkingen gelijk aan elkaar stelt, kunt u de bewegingsvergelijkingen voor de slinger afleiden.

De derde wet van Newton stelt dat elke actie een reactie van gelijke kracht heeft. Deze wet werkt met de eerste wet die aantoont dat hoewel de massa en zwaartekracht de verticale component van de snaarspanningsvector opheffen, niets de horizontale component opheft. Deze wet laat zien dat de krachten die op een slinger werken elkaar kunnen opheffen.

Natuurkundigen gebruiken Newtons eerste, tweede en derde wetten om te bewijzen dat de horizontale snaarspanning de slinger beweegt zonder rekening te houden met massa of zwaartekracht. De wetten van een eenvoudige slinger volgen de ideeën van de drie bewegingswetten van Newton.