Hoe de hoeksnelheid te berekenen

Inhoud

• De basis van beweging
• De hoeksnelheidsvergelijking
• Rotationele bewegingsvergelijkingen
• Gerelateerde hoeveelheden en uitdrukkingen
• Hoeksnelheid versus lineaire snelheid

In het dagelijkse discours worden "snelheid" en "snelheid" vaak door elkaar gebruikt. In de natuurkunde hebben deze termen echter specifieke en verschillende betekenissen. "Snelheid" is de verplaatsingssnelheid van een object in de ruimte en wordt alleen gegeven door een nummer met specifieke eenheden (vaak in meters per seconde of mijl per uur). Snelheid daarentegen is een snelheid gekoppeld aan een richting. Snelheid wordt dan een scalaire grootheid genoemd, terwijl snelheid een vectorgrootheid is.

Wanneer een auto langs een snelweg snelt of een honkbal door de lucht zoeft, wordt de snelheid van deze objecten gemeten ten opzichte van de grond, terwijl de snelheid meer informatie bevat. Als u bijvoorbeeld in een auto zit met 70 mijl per uur op de Interstate 95 aan de oostkust van de Verenigde Staten, is het ook handig om te weten of deze naar het noordoosten in de richting van Boston of het zuiden in de richting van Florida gaat. Met het honkbal wilt u misschien weten of zijn y-coördinaat sneller verandert dan zijn x-coördinaat (een vliegbal) of dat het omgekeerde waar is (een lijnaandrijving). Maar hoe zit het met het spinnen van de banden of de rotatie (spin) van het honkbal terwijl de auto en de bal richting hun uiteindelijke bestemming rijden? Voor dit soort vragen biedt natuurkunde het concept van hoeksnelheid.

De basis van beweging

Dingen bewegen op drie belangrijke manieren door driedimensionale fysieke ruimte: vertaling en rotatie. Vertaling is de verplaatsing van het hele object van de ene locatie naar de andere, zoals een auto die van New York City naar Los Angeles rijdt. Rotatie is daarentegen de cyclische beweging van een object rond een vast punt. Veel objecten, zoals het honkbal in het bovenstaande voorbeeld, vertonen beide soorten beweging tegelijkertijd; terwijl een vliegbal door de lucht van de thuisplaat naar het buitenveldhek bewoog, draait hij ook met een bepaalde snelheid rond zijn eigen centrum.

Het beschrijven van deze twee soorten beweging wordt behandeld als afzonderlijke fysische problemen; dat wil zeggen, bij het berekenen van de afstand die de bal door de lucht reist op basis van zaken als zijn initiële lanceerhoek en de snelheid waarmee hij de knuppel verlaat, kunt u de rotatie negeren en bij het berekenen van de rotatie kunt u hem behandelen als zittend in één plaats voor huidige doeleinden.

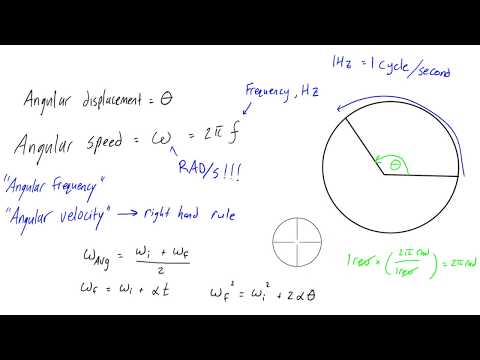
De hoeksnelheidsvergelijking

Ten eerste, als je het over "hoekige" dingen hebt, of het nu snelheid of een andere fysieke hoeveelheid is, erken dan dat, omdat je met hoeken te maken hebt, je het hebt over reizen in cirkels of delen daarvan. Je herinnert je misschien uit geometrie of trigonometrie dat de omtrek van een cirkel de diameter maal de constante pi is, of πd. (De waarde van pi is ongeveer 3.14159.) Dit wordt vaker uitgedrukt in termen van de cirkelsradius r, dat is de helft van de diameter, waardoor de omtrek 2nr.

Bovendien heb je waarschijnlijk ergens onderweg geleerd dat een cirkel bestaat uit 360 graden (360 °). Als u een afstand S langs een cirkel verplaatst, dan is de hoekverplaatsing θ gelijk aan S / r. Eén volledige revolutie geeft dan 2πr / r, waardoor er net 2π overblijft. Dat betekent dat hoeken kleiner dan 360 ° kunnen worden uitgedrukt in termen van pi, of met andere woorden, als radialen.

Als je al deze informatie bij elkaar neemt, kun je hoeken, of delen van een cirkel, in andere eenheden dan graden uitdrukken:

360 ° = (2π) radialen, of

1 radiaal = (360 ° / 2π) = 57.3 °,

Terwijl de lineaire snelheid wordt uitgedrukt in lengte per tijdseenheid, wordt de hoeksnelheid gemeten in radialen per tijdseenheid, meestal per seconde.

Als je weet dat een deeltje met een snelheid in een cirkelvormig pad beweegt v op een afstand r vanuit het middelpunt van de cirkel, met de richting van v altijd loodrecht op de straal van de cirkel, dan kan de hoeksnelheid worden geschreven

ω = v / r,

waar ω is de Griekse letter omega. Hoeksnelheidseenheden zijn radialen per seconde; u kunt deze eenheid ook als "wederzijdse seconden" behandelen, omdat v / r m / s oplevert gedeeld door m, of s^-1, wat betekent dat radialen technisch een eenheidloze hoeveelheid zijn.

Rotationele bewegingsvergelijkingen

De formule voor hoekversnelling wordt op dezelfde essentiële manier afgeleid als de formule voor hoeksnelheid: het is slechts de lineaire versnelling in een richting loodrecht op een straal van de cirkel (equivalent, de versnelling langs een raaklijn aan het cirkelvormige pad op elk punt) verdeeld door de straal van de cirkel of het gedeelte van een cirkel, dat is:

α = a_t/ r

Dit wordt ook gegeven door:

α = ω / t

omdat voor cirkelvormige beweging, een_t = ωr / t = v / t.

α, zoals u waarschijnlijk weet, is de Griekse letter 'alpha'. Het subscript "t" geeft hier "raaklijn" aan.

Vreemd genoeg heeft rotatiebeweging echter een ander soort versnelling, centripetale ("middelzoekende") versnelling genoemd. Dit wordt gegeven door de uitdrukking:

een_c = v²/ r

Deze versnelling is gericht op het punt waarrond het object in kwestie draait. Dit lijkt misschien vreemd, omdat het object sinds de straal niet dichter bij dit centrale punt komt r is gemaakt. Zie centripetale versnelling als een vrije val waarbij er geen gevaar is dat het object de grond raakt, omdat de kracht die het object ernaartoe trekt (meestal zwaartekracht) precies wordt gecompenseerd door de tangentiële (lineaire) versnelling die wordt beschreven door de eerste vergelijking in deze sectie. Als een_c waren niet gelijk aan een_t, zou het object in de ruimte vliegen of snel in het midden van de cirkel botsen.

Gerelateerde hoeveelheden en uitdrukkingen

Hoewel de hoeksnelheid meestal wordt uitgedrukt, zoals opgemerkt, in radialen per seconde, kunnen er gevallen zijn waarin het de voorkeur of nodig is om in plaats daarvan graden per radius te gebruiken of omgekeerd om van graden naar radialen om te zetten voordat een probleem wordt opgelost.

Stel dat u werd verteld dat een lichtbron elke seconde met een constante snelheid 90 ° roteert. Wat is zijn hoeksnelheid in radialen?

Onthoud eerst dat 2π radialen = 360 ° en stel een verhouding in:

360 / 2π = 90 / x

360x = 180π

x = ω = π / 2

Het antwoord is halve pi radialen per seconde.

Als je verder zou horen dat de lichtstraal een bereik van 10 meter heeft, wat zou dan het puntje van de lineaire snelheid van de bundel zijn? v, zijn hoekversnelling α en zijn centripetale versnelling een_c?

Op te lossen voor v, van boven, v = ωr, waar ω = π / 2 en r = 10m:

(π / 2) (10) = 5π rad / s = 15,7 m / s

Op te lossen voor α, voeg gewoon een andere tijdseenheid toe aan de noemer:

α = 5π rad / s²

(Merk op dat dit alleen werkt voor problemen waarbij de hoeksnelheid constant is.)

Ten slotte, ook van boven, een_c = v²/ r = (15.7)²/ 10 = 24,65 m / s².

Hoeksnelheid versus lineaire snelheid

Voortbouwend op het vorige probleem, stel je jezelf voor op een zeer grote draaimolen, een met een onwaarschijnlijke straal van 10 kilometer (10.000 meter). Deze draaimolen maakt elke 1 minuut en 40 seconden of elke 100 seconden een volledige revolutie.

Een gevolg van het verschil tussen hoeksnelheid, die onafhankelijk is van de afstand tot de rotatieas, en lineaire cirkelvormige snelheid, wat niet het geval is, is dat twee mensen dezelfde ervaren ω kan een enorm verschillende fysieke ervaring ondergaan. Als je toevallig 1 meter van het midden bent en deze vermeende, massieve draaimolen is je lineaire (tangentiële) snelheid:

ωr = (2π rad / 100 s) (1 m) = 0,0628 m / s, of 6,29 cm (minder dan 3 inch) per seconde.

Maar als je op de rand van dit monster bent, is je lineaire snelheid:

ωr = (2π rad / 100 s) (10.000 m) = 628 m / s. Dat is ongeveer 1,406 mijl per uur, sneller dan een kogel. Wacht even!