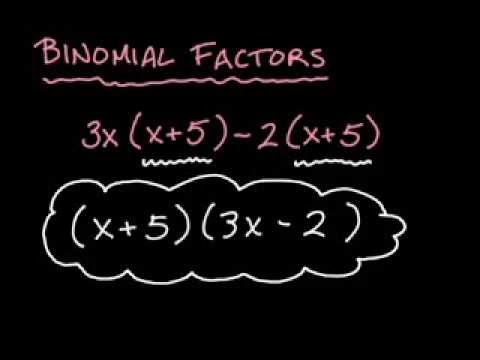
Inhoud
Polynomen zijn vaak het product van kleinere polynoomfactoren. Binomiale factoren zijn polynoomfactoren die exact twee termen hebben. Binomiale factoren zijn interessant omdat binomials eenvoudig op te lossen zijn en de wortels van de binomiale factoren dezelfde zijn als de wortels van de polynoom. Factoring van een polynoom is de eerste stap om zijn wortels te vinden.
Graphing
Het in kaart brengen van een polynoom is een goede eerste stap bij het vinden van de factoren. De punten waar de grafische curve de X-as kruist, zijn wortels van de polynoom. Als de curve de as kruist op punt p, dan is p een wortel van de polynoom en is X - p een factor van de polynoom. U moet de factoren controleren die u uit een grafiek haalt, omdat het gemakkelijk is om een meting uit een grafiek te verwarren. Het is ook gemakkelijk om meerdere wortels in een grafiek te missen.
Kandidaatfactoren
De kandidaat binomiale factoren voor een polynoom zijn samengesteld uit de combinaties van de factoren van de eerste en laatste getallen in het polynoom. 3X ^ 2 - 18X - 15 heeft bijvoorbeeld als eerste nummer 3, met factoren 1 en 3, en als laatste nummer 15, met factoren 1, 3, 5 en 15. De kandidaat-factoren zijn X - 1, X + 1 , X - 3, X + 3, X - 5, X + 5, X - 15, X + 15, 3X - 1, 3X + 1, 3X - 3, 3X + 3, 3X - 5, 3X + 5, 3X - 15 en 3X + 15.
De factoren vinden
Als we elk van de kandidaat-factoren proberen, zien we dat 3X + 3 en X - 5 3X ^ 2 - 18X - 15 delen zonder rest. Dus 3X ^ 2 - 18X - 15 = (3X + 3) (X - 5). Merk op dat 3X + 3 een factor is die we zouden hebben gemist als we alleen op de grafiek vertrouwden. De curve kruist de X-as op -1, wat suggereert dat X - 1 een factor is. Natuurlijk is het echt omdat 3X ^ 2 - 18X - 15 = 3 (X + 1) (X - 5).
De wortels vinden
Als je eenmaal de binomiale factoren hebt, is het gemakkelijk om de wortels van een polynoom te vinden - de wortels van het polynoom zijn dezelfde als de wortels van de binomials. De wortels van 3X ^ 2 - 18X - 15 = 0 zijn bijvoorbeeld niet duidelijk, maar als u weet dat 3X ^ 2 - 18X - 15 = (3X + 3) (X - 5), de wortel van 3X + 3 = 0 is X = -1 en de wortel van X - 5 = 0 is X = 5.