Inhoud
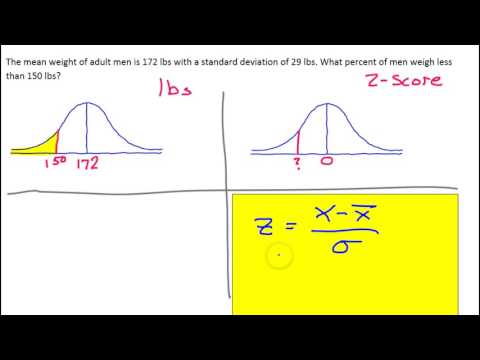
Statistici gebruiken de term "normaal" om een reeks getallen te beschrijven waarvan de frequentieverdeling klokvormig en symmetrisch is aan weerszijden van de gemiddelde waarde. Ze gebruiken ook een waarde die bekend staat als standaarddeviatie om de spreiding van de set te meten. Je kunt elk getal uit een dergelijke gegevensset nemen en een wiskundige bewerking uitvoeren om het te veranderen in een Z-score, die laat zien hoe ver die waarde verwijderd is van het gemiddelde in veelvouden van de standaarddeviatie. Ervan uitgaande dat u uw Z-score al kent, kunt u deze gebruiken om het percentage waarden in uw verzameling getallen binnen een bepaalde regio te vinden.
Bespreek uw specifieke statistische vereisten met een docent of collega, en bepaal of u het percentage cijfers in uw gegevensset wilt weten dat hoger of lager is dan de waarde die aan uw Z-score is gekoppeld. Als u bijvoorbeeld een verzameling SAT-scores voor studenten hebt met een perfecte normale verdeling, wilt u misschien weten welk percentage studenten boven de 2.000 heeft gescoord, dat u hebt berekend met een overeenkomstige Z-score van 2.85.
Open een statistisch naslagwerk naar de z-tabel en scan de meest linkse kolom van de tabel totdat u de eerste twee cijfers van uw Z-score ziet. Hiermee wordt de rij in de tabel weergegeven die u nodig hebt om uw percentage te vinden. Bijvoorbeeld, voor uw SAT Z-score van 2,85, zou u de cijfers "2.8" vinden in de meest linkse kolom en zien dat deze overeenkomt met de 29e rij.
Zoek het derde en laatste cijfer van uw z-score in de bovenste rij van de tabel. Hiermee wordt de juiste kolom in de tabel weergegeven. In het geval van het SAT-voorbeeld heeft de Z-score een derde cijfer van "0,05", dus u zou deze waarde langs de bovenste rij vinden en zien dat deze overeenkomt met de zesde kolom.
Zoek naar het kruispunt in het hoofdgedeelte van de tabel waar de rij en kolom die u zojuist hebt geïdentificeerd elkaar ontmoeten. Hier vindt u de procentuele waarde die aan uw Z-score is gekoppeld. In het SAT-voorbeeld vindt u het snijpunt van de 29e rij en de zesde kolom en vindt u de waarde daar is 0,4978.
Trek de waarde die u zojuist hebt gevonden af van 0,5, als u het percentage gegevens in uw set wilt berekenen dat groter is dan de waarde die u hebt gebruikt om uw Z-score te bepalen. De berekening in het geval van het SAT-voorbeeld zou daarom 0,5 - 0,4978 = 0,0022 zijn.
Vermenigvuldig de uitkomst van uw laatste berekening met 100 om er een percentage van te maken. Het resultaat is het percentage waarden in uw set dat hoger is dan de waarde die u in uw Z-score heeft omgezet. In het geval van het voorbeeld vermenigvuldigt u 0,0022 met 100 en concludeert u dat 0,22 procent van de studenten een SAT-score van meer dan 2000 had.
Trek de waarde af die u zojuist hebt afgeleid van 100 om het percentage waarden in uw gegevensset te berekenen die lager zijn dan de waarde die u hebt geconverteerd naar een Z-score. In het voorbeeld zou je 100 min 0,22 berekenen en concluderen dat 99,78 procent van de studenten onder de 2000 scoort.