Inhoud
Een verhouding is een vergelijking tussen een paar getallen, en hoewel u deze meestal kunt verkrijgen door directe metingen, moet u mogelijk enkele berekeningen uitvoeren om het nuttig te maken. Deze berekeningen worden schaalvergroting genoemd, en ze kunnen belangrijk zijn wanneer je iets doet zoals het aanpassen van een recept voor verschillende aantallen mensen. Bij het vergelijken van getallen in een verhouding, is het belangrijk om te weten wat ze vertegenwoordigen. De getallen kunnen twee delen van een geheel vertegenwoordigen, of een van de getallen kan een deel van een geheel vertegenwoordigen, terwijl het andere getal het geheel zelf vertegenwoordigt.
Een verhouding uitdrukken
Wiskundigen en wetenschappers gebruiken een van de drie conventies om een verhouding uit te drukken. Stel dat u twee nummers A en B hebt. U kunt de verhouding daartussen uitdrukken als:
Als je de verhouding hardop leest, zeg je altijd "A tot B." De term voor A is de antecedent en de term voor B is de consequent.
Overweeg bijvoorbeeld een basisschoolklasse met 32 studenten, van wie 17 meisjes en 15 jongens. De verhouding tussen meisjes en jongens kan worden geschreven als 17:15, 17 tot 15 of 17/15, terwijl de verhouding tussen jongens en meisjes 15:17, 15 tot 17 of 15/17 is. Het klaslokaal heeft 32 studenten, dus de verhouding tussen meisjes en het totale aantal studenten is 17:32 en de verhouding tussen jongens en het totale aantal studenten is 15:32.
Wanneer u een deel van een geheel met het geheel vergelijkt, kunt u de verhouding omzetten in een percentage door deze in fractionele vorm uit te drukken, het antecedent te delen door het gevolg en te vermenigvuldigen met 100. In ons voorbeeld vinden we dat de klasse 17/32 x is 100 = 53% vrouwelijk en 15/32 x 100 = 47% mannelijk. In percentages is de verhouding meisjes en jongens 53:47 en de verhouding jongens en meisjes 47:53.
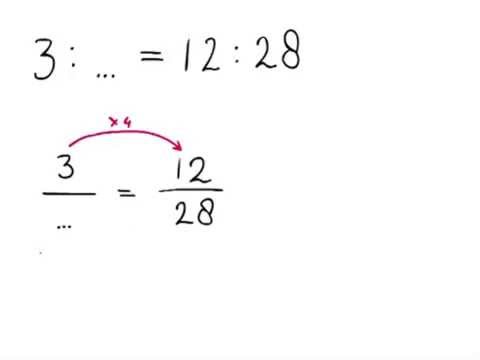
Een verhouding schalen
U schaalt een verhouding door zowel het antecedent als het consequent met hetzelfde getal te vermenigvuldigen. In het bovenstaande voorbeeld hebben we de verhouding geschaald door te vermenigvuldigen met 100 om ons percentages te geven, die vaak nuttiger zijn dan ruwe getallen. Koks moeten vaak verhoudingen opschalen om recepten aan te passen voor verschillende aantallen mensen.
Bijvoorbeeld, een recept bedoeld om 4 personen te voeden vraagt om 2 kopjes soepmix toe te voegen aan 6 kopjes water. De verhouding soepmix tot water is daarom 2: 6. Als een kok deze soep voor 12 personen wil maken, moet hij of zij elke term met 3 vermenigvuldigen, omdat 12 gedeeld door 4 = 3. De verhouding wordt dan 6:18. De kok moet 6 kopjes soepmix toevoegen aan 12 kopjes water.
Vereenvoudiging van een ratio
Wanneer een verhouding twee grote getallen vergelijkt, is het vaak handig om het te vereenvoudigen door het antecedent en bijgevolg te delen door een gemeenschappelijke factor. U kunt bijvoorbeeld de verhouding 128: 512 vereenvoudigen door elke term te delen door 128. Dit levert de handiger verhouding 1: 4 op.
Overweeg ter illustratie een referendum over een voorstel om aanvalswapens te verbieden. Tienduizend mensen stemden in een bepaald stembureau, en toen de resultaten werden opgeteld, bleken 4.800 mensen op de stelling te stemmen, 3.200 stemmen ertegen en 2.000 waren onbeslist. De verhouding tussen die voor de propositie en die ertegen was 4.800: 3.200. Vereenvoudig dit door elke term te delen door 1600 om te ontdekken dat de verhouding tussen die voor de propositie en die ertegen 3 was. Aan de andere kant was de verhouding van degenen die een mening hadden over de propositie tot degenen die dat niet deden 8.000: 2.000. of 4: 1 na het delen van elke term door 2.000.
Bij het rapporteren van stemresultaten, zetten nieuwsmedia de verhoudingen vaak om in percentages. In dit geval was het percentage van die voor de propositie 4.800 / 10.000 = 48/100 = 0.48 x 100 = 48%. Het percentage kiezers tegen de propositie was 3.200 / 10.000 = 32/100 = 0.32 x 100 = 32%, en het percentage kiezers dat onbeslist was, was 2.000 / 10.000 = 20/100 = 0.2 x 100 = 20%.