
Inhoud
In de geometrie is een achthoek een veelhoek met acht zijden. Een regelmatige achthoek heeft acht gelijke zijden en gelijke hoeken. De regelmatige achthoek wordt algemeen herkend aan stopborden. Een octaëder is een achtzijdige veelvlak. Een regelmatige octaëder heeft acht driehoeken met randen van gelijke lengte. Het zijn in feite twee vierkante piramides die elkaar ontmoeten aan hun basis.
Octagon Area Formula
De formule voor het gebied van een regelmatige achthoek met zijden van lengte "a" is 2 (1 + sqrt (2)) a ^ 2, waarbij "sqrt" de vierkantswortel aangeeft.
Afleiding
Een achthoek kan worden gezien als 4 rechthoeken, een vierkant in het midden en vier gelijkbenige driehoeken in de hoeken.
Het vierkant heeft een oppervlakte a ^ 2.
De driehoeken hebben zijden a, a / sqrt (2) en a / sqrt (2), volgens de stelling van Pythagoras. Daarom heeft elk een oppervlakte van ^ 2/4.
De rechthoeken hebben de oppervlakte a * a / sqrt (2).
De som van deze 9 gebieden is 2a ^ 2 (1 + sqrt (2)).
Octahedron-volumeformule
De formule voor het volume van een regelmatige octaëder van zijden "a" is een ^ 3 * sqrt (2) / 3.
Afleiding
Het gebied van een vierzijdige piramide is het gebied van basis * hoogte / 3. Het gebied van een regelmatige achthoek is daarom 2 * basis * hoogte / 3.
Base = a ^ 2 triviaal.
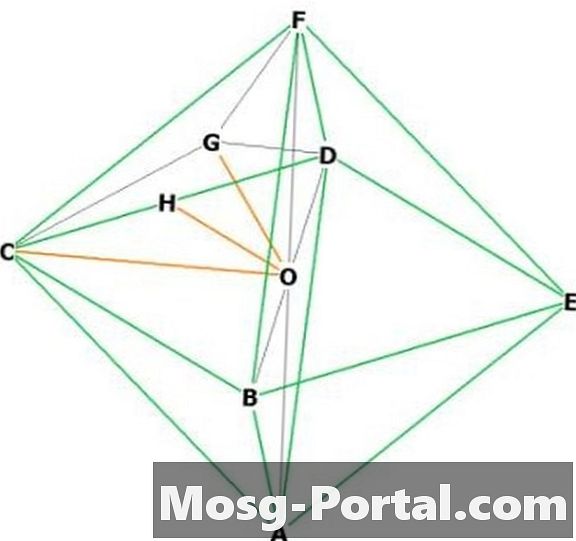
Kies twee aangrenzende hoekpunten, zeg "F" en "C." "O" staat in het midden. FOC is een gelijkbenige rechthoekige driehoek met basis "a", dus OC en OF hebben lengte a / sqrt (2) volgens de stelling van Pythagoras. Dus hoogte = a / sqrt (2).
Het volume van een gewone octaëder is dus 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Oppervlakte
Het regelmatige octaëderoppervlak is het gebied van een gelijkzijdige driehoek van zijde "a" maal 8 gezichten.
Om de stelling van Pythagoras te gebruiken, laat je een lijn van de top naar de basis vallen. Dit creëert twee rechte driehoeken, met de hypotenusa van lengte "a" en één zijde lengte "a / 2". Daarom moet de derde zijde sqrt = sqrt (3) a / 2 zijn. Het gebied van een gelijkzijdige driehoek is dus hoogte * basis / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Met 8 zijden is de oppervlakte van een gewone octaëder 2 * sqrt (3) * a ^ 2.