Inhoud
- Mechanisch voordeel
- Wet van behoud van energie
- Differentiële katrol
- Newtons tweede wet
- Meer hangende blokken
Met katrollen kunnen verschillende interessante situaties worden opgezet om studenten te laten begrijpen wat Newtons tweede bewegingswet, de wet van behoud van energie en de definitie van werk in de fysica is. Een bijzonder leerzame situatie kan worden gevonden in wat een differentiële poelie wordt genoemd, een gebruikelijk gereedschap dat wordt gebruikt in monteurszaken voor zwaar tillen.
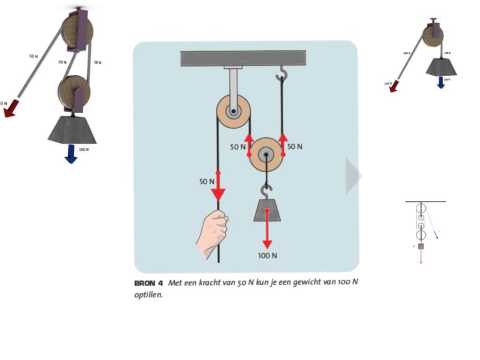
Mechanisch voordeel
Net als bij een hefboom verhoogt het vergroten van de afstand waarover een kracht wordt uitgeoefend vergeleken met de afstand waarop de last wordt opgeheven, het mechanische voordeel of hefboomwerking. Stel dat twee blokken katrollen worden gebruikt. Men hecht aan een lading; men hecht boven aan een steun. Als de lading X-eenheden moet worden opgetild, moet het onderste poelieblok ook X-eenheden omhoog brengen. Het poelieblok hierboven beweegt niet omhoog of omlaag. Daarom moet de afstand tussen de twee poelieblokken X-eenheden verkorten. De lengtes van de lijn tussen de twee poelieblokken moeten X-eenheden elk korter maken. Als er dergelijke Y-lijnen zijn, moet de trekker X --- Y-eenheden trekken om de lading X-eenheden op te tillen. De vereiste kracht is dus 1 / Y maal het gewicht van de lading. Het mechanische voordeel is naar verluidt Y: 1.
Wet van behoud van energie
Dit hefboomeffect is een gevolg van de wet van behoud van energie. Bedenk dat werk een vorm van energie is. Met werk bedoelen we de fysische definitie: kracht uitgeoefend op een belasting maal afstand waarover de belasting door de kracht wordt verplaatst. Dus als de belasting Z Newton is, moet de energie die nodig is om de X-eenheden op te tillen gelijk zijn aan het werk van de trekker. Met andere woorden, Z --- X moet gelijk zijn (kracht uitgeoefend door trekker) --- XY. Daarom is de kracht die wordt uitgeoefend door de trekker Z / Y.
Differentiële katrol
Een interessante vergelijking doet zich voor wanneer u van de lijn een doorlopende lus maakt en het blok dat aan de steun hangt twee katrollen heeft, de ene iets kleiner dan de andere. Stel ook dat de twee katrollen in het blok zijn bevestigd zodat ze samen roteren. Noem de stralen van de riemschijven "R" en "r", waarbij R> r.
Als de trekker voldoende lijn uittrekt om de vaste katrollen een rotatie te laten draaien, heeft hij 2 nR lijn uitgetrokken. De grotere riemschijf heeft dan 2πR lijn ingenomen van de last. De kleinere poelie is in dezelfde richting gedraaid en laat 2 nlijn lijn vrij naar de lading. Dus de belasting stijgt 2πR-2πr. Het mechanische voordeel is de getrokken afstand gedeeld door de opgetilde afstand, of 2πR / (2πR-2πr) = R / (R-r). Merk op dat als de stralen slechts 2 procent verschillen, het mechanische voordeel maar liefst 50 tegen 1 is.
Een dergelijke katrol wordt een differentiële katrol genoemd. Het is een veel voorkomend onderdeel in autoreparatiewerkplaatsen. Het heeft de interessante eigenschap dat de lijn die de trekker trekt los kan hangen terwijl een lading omhoog wordt gehouden, omdat er altijd voldoende wrijving is die de tegengestelde krachten op de twee riemschijven verhinderen te draaien.
Newtons tweede wet


Stel dat twee blokken zijn verbonden, en één, noem het M1, hangt aan een riemschijf. Hoe snel zullen ze versnellen? Newtons tweede wet heeft betrekking op kracht en versnelling: F = ma. De massa van de twee blokken is bekend (M1 + M2). Versnelling is onbekend. Kracht is bekend uit de zwaartekracht op M1: F = ma = M1 --- g, waarbij g de zwaartekrachtversnelling aan het aardoppervlak is.
Houd er rekening mee dat M1 en M2 samen worden versneld. Het vinden van hun versnelling, a, is nu slechts een kwestie van substitutie in de formule F = ma: M1 --- g = (M1 + M2) a. Natuurlijk, als wrijving tussen M2 en de tafel een van de krachten is waar F = M1 --- g tegen moet zijn, dan wordt die kracht ook gemakkelijk aan de rechterkant van de vergelijking toegevoegd, vóór versnelling, a, is opgelost voor.
Meer hangende blokken

Wat als beide blokken hangen? Dan heeft de linkerkant van de vergelijking twee toevoegingen in plaats van slechts één. De lichtere zal in de tegenovergestelde richting van de resulterende kracht reizen, omdat de grotere massa de richting van het twee-massasysteem bepaalt; daarom moet de zwaartekracht op de kleinere massa worden afgetrokken. Stel dat M2> M1. Vervolgens verandert de linkerkant links van M1 --- g in M2 --- g-M1 --- g. De rechterhand blijft hetzelfde: (M1 + M2) a. Versnelling, a, wordt dan triviaal rekenkundig opgelost.