Inhoud
Alle juiste driehoeken hebben 90 graden of rechte hoeken. Ze worden in de wiskunde gebruikt voor speciale berekeningen, inclusief het vinden van de exacte afstand tussen twee punten. Rechte driehoeken kunnen je ook helpen om hoogten en afstanden te vinden die erg groot of anderszins moeilijk te meten zijn. Rechte driehoeken hebben veel speciale eigenschappen die de basis vormen van trigonometrie.
Anatomie van een juiste driehoek
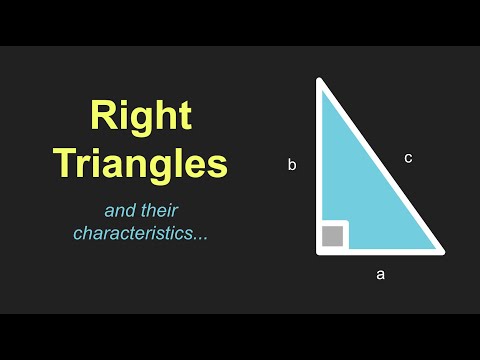
De twee kortere zijden van een rechte hoek worden benen genoemd. Ze worden meestal aangeduid met de letters "a" en "b". De derde zijde, die tegenover de hoek van 90 graden staat, wordt de hypotenusa genoemd en wordt meestal aangeduid met "c".
De stelling van Pythagoras
De stelling van Pythagoras stelt dat de som van elk van de kwadraten van een rechte driehoekige beenlengte gelijk is aan de lengte van het kwadraat van de hypotenusa. Met andere woorden, a ^ 2 + b ^ 2 = c ^ 2, waarbij "a" en "b" benen zijn en "c" de hypotenusa is. Als u twee zijden van een rechthoekige driehoek kent, kan de stelling worden toegepast om de derde zijde te vinden. Dit wordt in veel gevallen gebruikt om moeilijk te meten afstanden of lengtes te vinden. Als je bijvoorbeeld weet dat je 10 blokken naar het zuiden rijdt, dan 6 blokken naar het oosten om van huis naar de winkel te komen, maar je wilt weten wat de directe afstand tussen huis en de winkel is. Je kunt 10 ^ 2 + 6 ^ 2 = (de directe afstand) ^ 2 instellen om te zien dat het ongeveer 12 blokken is hemelsbreed.
45-45-90 Driehoeken
Een van de speciale rechter driehoeken is de 45-45-90 driehoek. Het wordt gevormd door een diagonale lijn te trekken van een hoek naar de tegenoverliggende hoek van een vierkant. Het is de enige rechthoekige driehoek waar beide benen exact dezelfde lengte meten. Het is dus het enige type rechthoekige driehoek die ook een gelijkbenige driehoek is. De naam 45-45-90 komt van de afmetingen van de binnenhoeken. Er is de vereiste hoek van 90 graden en de kleinere hoeken meten beide 45 graden. De benen en de hypotenusa vertonen altijd een verhouding van 1: √2. Voor deze driehoek hoeft u dus alleen de lengte van één zijde te kennen om de andere twee lengtes te vinden. De lengte van de benen is gelijk en de lengte van de hypotenusa is gelijk aan de lengte van een been maal √2.
30-60-90 Driehoeken
Net als bij de driehoek 45-45-90, krijgt de driehoek 30-60-90 zijn naam omdat de binnenhoeken 30, 60 en 90 graden meten. Deze driehoek wordt gevormd door een gelijkzijdige driehoek in twee te snijden. De 30-60-90 driehoekenzijden vormen ook een constante verhouding van 1: √3: 2. Het korte been staat recht tegenover de hoek van 30 graden en meet altijd de helft van de lengte van de hypotenusa, die tegenover de Hoek van 90 graden. Het langere been, dat tegenover de hoek van 60 graden staat, meet de lengte van de korte beentijden √3, of de helft van de hypotenusa-tijden √3. Voor deze driehoek hoeft u dus alleen de lengte van één zijde te kennen om de lengtes van de andere twee zijden te vinden.